―しがない農学徒の雑記帳―

項目

• TOP
• 生物学、統計学、その他色々
• 日記
• リンク集

棒グラフと箱髭図の見方

生物学では実験により得られたデータを視覚化するのに棒グラフや箱髭図が用いられます。棒グラフには誤差棒が付き物ですし、箱髭図にはその名の通り箱や髭が生えていますが、その意味を理解している人は多くないと思います。そこで本項ではその意味するところを説明したいと思います。尚、本文に先立って、あくまでも棒グラフや箱髭図は次に示すヒストグラムを簡略化したものであり、本来は一番最初に生データを見て、次にヒストグラムを見て、その次に棒グラフや箱髭図を見るべきだと筆者は思っている事を述べておきます。

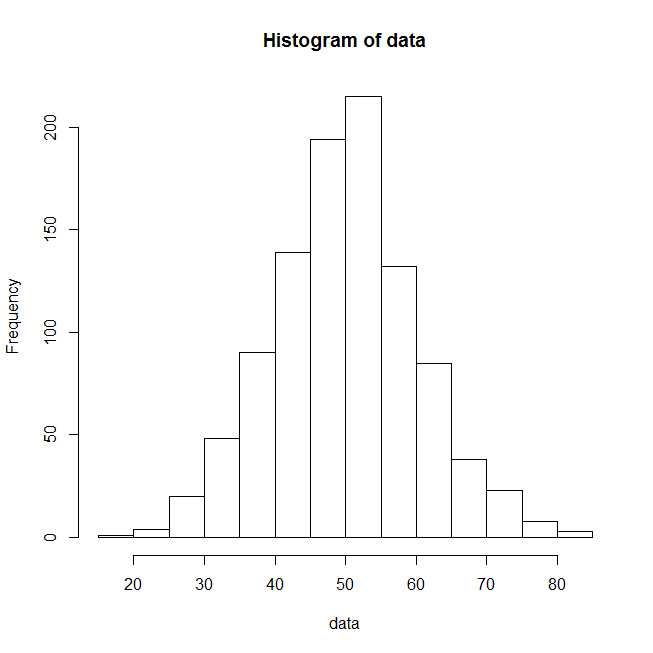
まずは棒グラフから。棒グラフは棒と誤差棒より構成されます。棒の高さはデータの平均値を意味します。誤差棒は多くの場合、平均値±標準偏差（SD）の範囲か、または、平均値±標準誤差（SE）の範囲に線が引かれます。

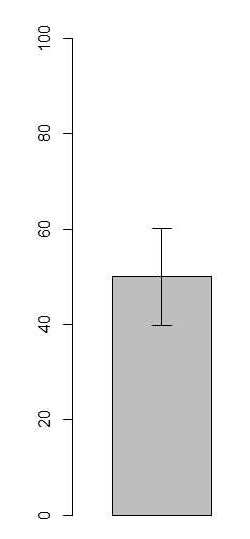
平均値 ± SD

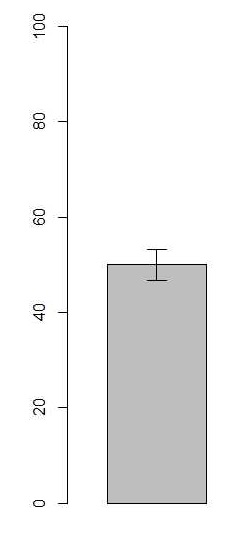
平均値 ± SE

この誤差棒の意味するところですが、SD の方は、データが正規分布に従っている場合、平均値 ± SD の範囲内にデータの約 70% が存在する事を意味します。 SE の場合は、同様の条件において平均値 ± SE の範囲内に母平均が存在する確率が約 70% であることを意味します。このように、SD と SE は意味するものが全く異なりますので、自分が棒グラフを描く場合は、何を主張したいかによって使い分ける必要があるかと思います。生物学で多くの場合、対照群と処理群の間における母平均の差に興味があると思われますが、これはおそらく誤差棒の長さとか被り具合では判別できず、統計検定の結果を読まないと理解できないと思います。そこで消去法的ですが、SD を表示した方が良いのではないかと筆者は思います。バラツキが小さく見えて都合が良いから SE の方を使う、というのは断じて違います。

次は箱髭図（はこひげず）です。箱髭図は長方形、真ん中の太線、および上下に伸びる髭より構成されます。長方形の下辺は小さい方から数えて 4 分の 1 の位置を、太線は真ん中の順位の位置（あるいは中央値）を、そして長方形の上辺は小さいほうから数えて 4 分の 3 の位置を示します。長方形、あるいは箱の長さを四分位範囲 (IQR) といいます。髭の長さは、長くて 1.5 × IQR です。どういう事かというと、上に伸びる髭は、箱の上辺より min( max(データ), 箱の上辺 ＋ 1.5 × IQR) の高さまで伸びています。下に伸びる髭は、箱の下辺より、max( min(データ), 箱の下辺 － 1.5 × IQR) の高さまで伸びています。もしも箱の上辺 ＋ 1.5 × IQR よりも大きいデータがある場合は、髭の端よりも上側のデータが個別に打点されます。逆に、もしも箱の下辺 － 1.5 × IQR よりも小さいデータがある場合は、髭の端よりも下側にあるデータが個別に打点されます。なお、max( ) は引数の中で他のどれよりも小さくないもの、min( ) は引数の中で他のどれよりも大きくないものを意味します。引数とは関数の括弧 ( ) の中身です。。。

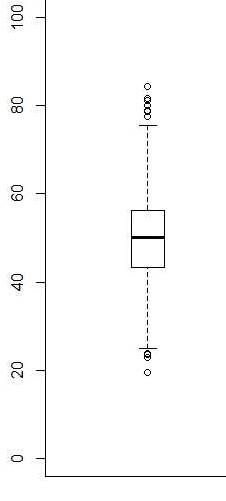
棒グラフと箱髭図をどう使い分けるかですが、誤差棒はデータが正規性を満たす時に意味を持つので、そのようなときに棒グラフを用い、そうでないときに箱髭図を用いるべきでしょう。ただし、データが正規性を満たすか否かは微妙な問題をはらんでいる様な気がしますので、個人的には、データのヒストグラムが左右対称ならば棒グラフを用い、左右非対称ならば箱髭図で視覚化する、という風に使い分ければ良いような気がします。